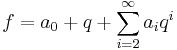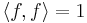Eigenform
An eigenform (meaning simultaneous Hecke eigenform) is a modular form which is an eigenvector for all Hecke operators Tm, m = 1, 2, 3, ….
Eigenforms fall into the realm of number theory, but can be found in other areas of math and science such as analysis, combinatorics, and physics.
Contents |
Normalization
There are two different normalizations for an eigenform (or for a modular form in general).
Algebraic normalization
An eigenform is said to be normalized when scaled so that the q-coefficient in its Fourier series is one:
where q = e2πiz, and ai, i ≥ 1 turn out to be the eigenvalues of f corresponding to the Hecke operator Ti. In the case of that f is not a cusp form, the eigenvalues can be given explicitly.[1]
Analytic normalization
As in any inner product space, an eigenform can be normalized with respect to its inner product:
Higher levels
In the case that the modular group is not the full SL(2,Z), there is not a Hecke operator for each n ∈ Z, and as such the definition of an eigenform is changed accordingly: an eigenform is a modular form which is a simultaneous eigenvector for all Hecke operators that act on the space.
- ^ Neal Koblitz. "III.5". Introduction to Elliptic Curves and Modular Forms.